Yenilenebilir enerji kaynağı olan rüzgar enerjisinden elektrik üretebilmek amacıyla “BİR RÜZGAR TÜRBİNİ HAREKET SİSTEMİ” isimli projem için tanıtıcı animasyon gösterimi ana hatlarıyla Animasyonda olduğu gibidir.Burada sistem çapının küçük olması nedeniyle kanatların kontrolü için dişli sistem kullanılmıştır.Kanatlar dişli sistem tarafından ana sisteme bağlı ( gavarnör dişli ) olarak otomatikman döngüsel hareket boyunca rüzgar akış yönüne göre optimum verimin alınacağı pozisyona gelmektedir.Rüzgarın yön değiştirmesi durumunda da bir hidrolik motor ve sistemi vasıtasıyla gavarnör dişli diyebileceğimiz merkezdeki dişlinin pozisyonu değiştirilerek kanatlarında ( kanat tahrik dişlileri bu gavarnör dişliden yönlendime aldıkları için ) yeni rüzgar akış yönüne göre optimum konum almaları sağlanabilecektir.

Ele aldığımız animasyon gösterimdeki sistemde kullanılan kanat kontrol dişlileri ve yönlendirici gavarnör dişli yerine halen günümüz teknolojisinde var olan birçok farlı kontrol ve tahrik sistemi kullanılabilir.Sistemin ana mantığı kanatlar vasıtasıyla rüzgar akış yönünde mümkün olduğunca etkin geniş yüzey alanı oluşturarak rüzgar enerjisini direnç ve sürtünme yöntemiyle absorbe etmektir.Öngördüğümüz sistem dikey eksenli bir rüzgar türbini olmakla birlikte animasyonda kullanılan dişli ve hidrolik ekipmanlar ile ( veya diğer kontrol sistemlerinden de yararlanılarak ) sistemin ve kanatların rüzgara karşı optimum düzeyde direnç oluşturacak şekilde konuşlandırmak ve yine bütün döngüsel hareket boyunca ve her hareket kademesinde kanatlardan optimum verimin alınacağı pozisyonlar için kanatları yönlendirmek, kontrol edebilmektir.

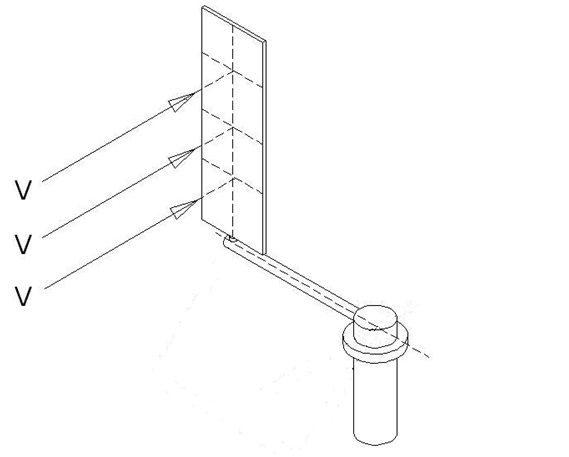
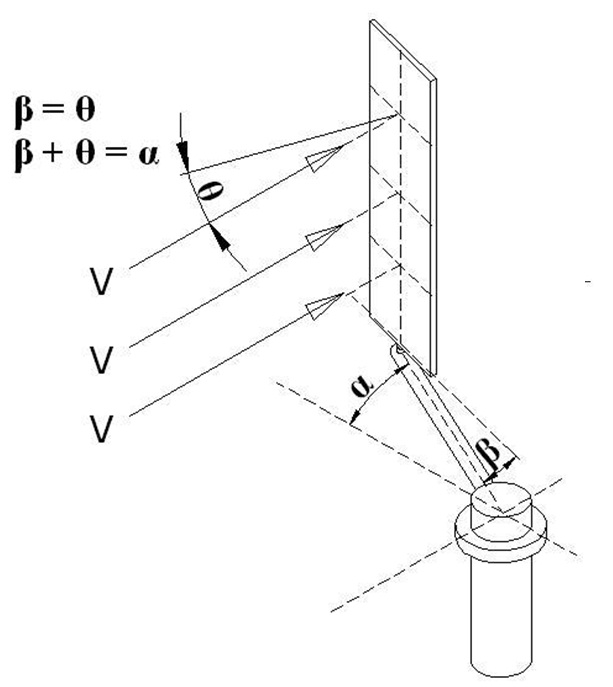
Şekil : 1’ deki rüzgar akış yönüne göre başlangıç konumunda olan kanatlar rüzgara dik açı yapmakta ve optimum direnç yüzeyi oluşturmaktadır.Sistemin hareketiyle birlikte ( Şekil : 2 ) başlayan döngüsel hareket boyunca kanadın vereceği optimum direnç açıları ( β değerleri ) “AÇI ANALİZLERİ” başlığı altında incelenmiştir.Buradaki değerlerden de anlaşılacağı üzere α = 0° sistemin ilk hali ve kanadın rüzgarı dik açı ile karşılama durumu başlangıç noktası olarak kabul edilirse ( Şekil : 1 ) sistem döndükçe kanat kendi kuvvet koluyla β açısı yapacak şekilde ( dişli,hidrolik,pnomatik—v.s gibi sistemlerle ) kontrol edilmeli, kanat anlık olarak β açısına yönlendirilmelidir.”AÇI ANALİZ” incelemesinde β açılarırı irdelenirken kanadın bağlı olduğu kuvvet kolu vasıtasıyla güç miline iletilen kuvvetin ancak kuvvet koluna dik açı ile etkileyen kuvvet vektörüyle ( Fd ) sağlanacağı göz önünde bulundurularak inceleme-araştırma yapılmıştır.

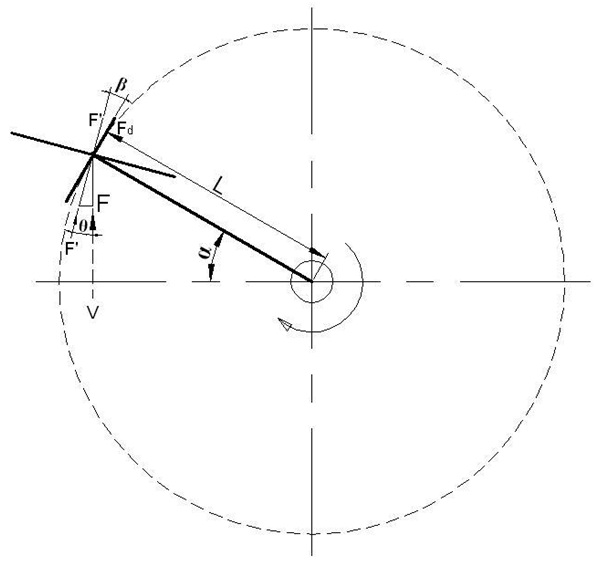
Şekil :3 de Fd ile ifade edilen vektör kolu kanat yüzeyinden elde edilecek F kuvvetinin L yarıçaplı kuvvet koluna dik olarak etki eden kuvvet vektör koludur.Böylece “AÇI ANALİZLERİ” sayfasındaki araştırma

Fd = F x Cos²β değerinin maksimum olduğu konumlar için incelenmiştir. Bütün daireselHareket boyunca yapılan incelemede maksimum Fd değerinin β = α/2 konumlarında sağlandığı görülmüştür.Bu datalardan yola çıkarak kurguladığımız sistemden bir tam devirde elde edilecek Fd kuvvet toplamı

İntegral hesabı sonucu Fd değeri bir devir için bulunur,biz bu bulunan değeri 2π ile bölersek dairesel harekette sabit kabul edebileceğimiz anlık bir Fd kuvvetini elde ederiz.Şimdi güç hesabı için hız faktörlerini incelemek yeterli olacaktır.

NOT : Hem bilgisayar ortamında hem de ölçekli kağıt üzerindeki çalışmalarımız aşağıda incelemenize sunulmuştur.Yukarıda ifade etmiş olduğumuz matematiksel
Fd = F ∫ Cos² α/2 dα ifadesinin sonucu
Fd = ½ F olarak bulunur ( bu sonuç anlık Fd kuvvetini bulmak için bir devir için bulduğumuz değerin 2π ile bölünmesiyle elde edilmiştir.)

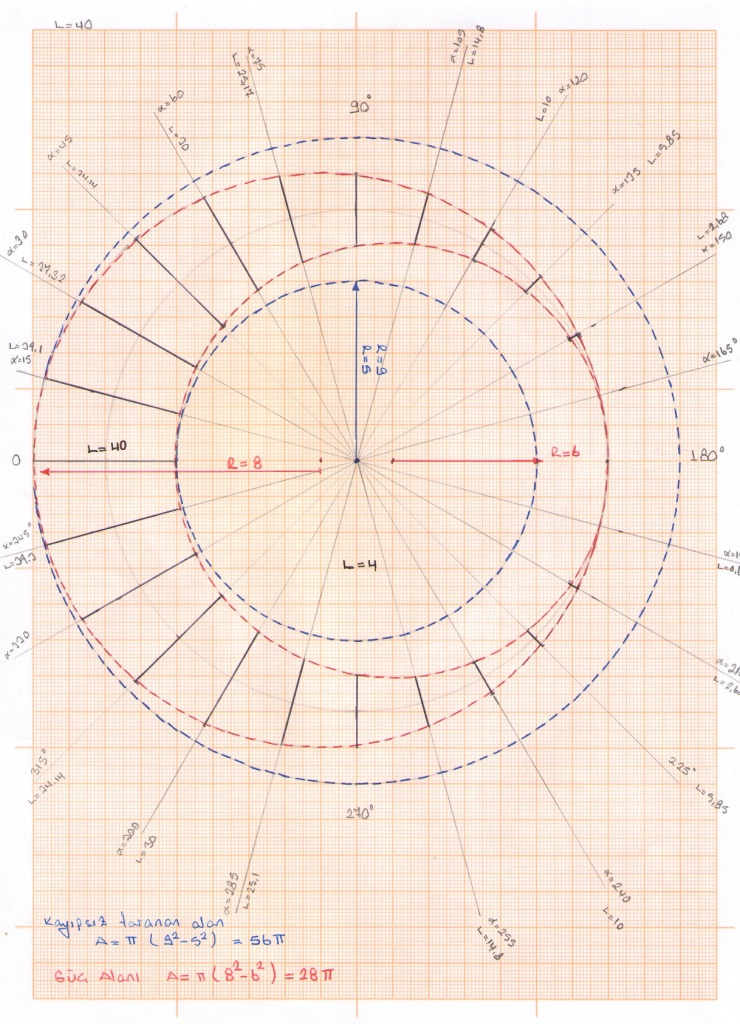
Bizim amacımız yukarıda ifade edilen matematiksel sonucun doğruluğunu test etmekti.Her iki çalışmada da dairesel hareketin değişik konumları için ( C=40 mm olarak ele alınarak ) hesaplamalar yapılarak bunlar grafik haline getirilmiştir. Her iki çalışmada da görülecegi üzere kanat dairesel hareket boyunca sabit tutulsaydı tarayacağı alan, bizim
β =α/2 bağlamında kontrollü kanat hareketleriyle bir devirde tarayacağı alanın iki katı olmaktadır.Matematiksel hesaplamayla pratikte gördügümüz değerler aynıdır.

Herbir kademede α açısına göre kanat üzerinde oluşacak ve kuvvet miline dik olarak etki edecek Fd kuvveti anlık olarak yukarıdaki matematiksel bağlamda hesaplanarak şekilde mavi ile gösterilen alan oluşturulmuştur.Bu şekilde pembe olarak görülen alan C = 40 mm olarak bütün dairesel hareketle taranabilecek alan olarak görürsek burada da Fd = ½ F oranını görürüz.

Bu ölçekli kağıt üzerindeki çalışmada da 56π değerinin 28π değerinin iki katı olduğu görülmektedir,aynı sonucu alıyoruz.