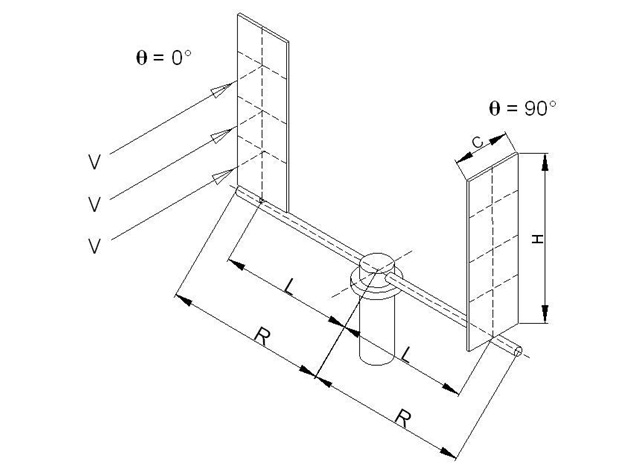
Şekil:1’ deki gibi rüzgar akış yönü kanada dik açı yaptığı ilk durum için ( ϴ = 0° )
F = ½ ρV²S
S = C x H
F = ½ ρV²CH
ρ = Havanın özgül ağırlığı
S = Bizim tespit ettiğimiz kanadın yüzey alanı
C = Kanadın genişliği
H = Kanadın yüksekliği
R = Sistemin yarıçapı
L = Kanat ekseninin mil merkez eksenine olan mesafesi
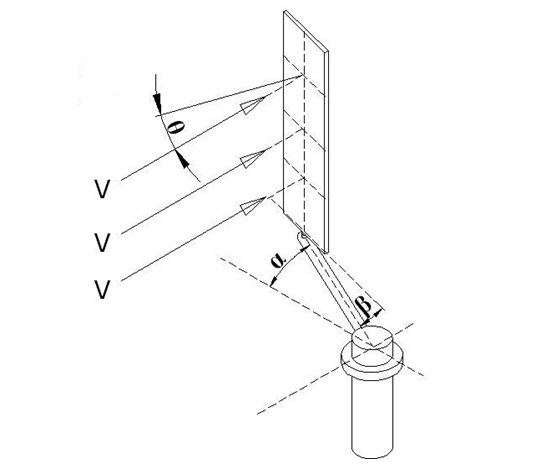
Rüzgar tepkimesiyle sistem hareket etmeye başladığında ilk konuma göre α açısı yapan sistem için kanat kendi kuvvet koluyla Şekil:2’ de gösterildiği üzere β açısı alacaktır.( Bütün döngüsel hareket boyunca
β = α/2 olacak şekilde kanat pozisyonlarını kontrol ediyoruz.)
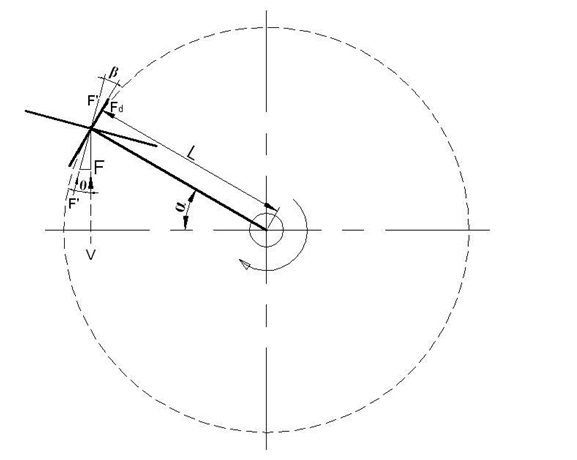
Şekil:2’ deki konum için oluşan kuvvet vektörlerin incelersek Şekil :3’ de Fd ifade edilen “L” kuvvet koluna dik açı yapan kuvvet vektör kolunu görürüz.Bu Fd kuvvet vektör kolu sistemi en etkili şekilde döndürmeye çalışan F kuvvetinin kuvvet koluna dik açı yapan vektörel koludur. F ile Fd arasında şöyle bir bağlantı vardır.
Fd = F Cos²α/2 İle ifade edilen bu bağlantı tüm dairesel hareket boyunca korunarak Şekil:4’ deki ölçekli kağıtla yapmış olduğumuz çalışmada görünen hilal şeklindeki alana tekabül eder.Bu pratik çalışmada görülmüştür ki Fd = F Cos²α/2 bağıntısı ile taranan alan (28π) Kanat açısı hiç değişmeden yapılan döngüsel hareketle taranan alanın (56π) yarısına tekabül etmektedir, yani toplam F/2 = Fd eşitliğini vermektedir.
Pratikte yapmış olduğumuz bu çalışmayı matematiksel ifadelerle doğrulamak istersek :
F = ½ ρV²S
F’ = F Cosϴ
Fd = F’ Cosβ
ϴ = α/2
β = α/2
Fd = F Cosϴ Cosβ
Fd = F ( Cos α/2) ( Cos α/2 )
Fd = F Cos²α/2
0---2π yani bir devir için toplam Fd kuvveti
Fd = F ∫ Cos²α/2 dα
Fd / F = ( (2π/2) + (Sin 2π/2) ) - ( (0/2) + ( Sin0/2 ) )
Fd = F π bulunur.
Bir anlık Fd kuvvet vektör kolunun F kuvvetine bağlı değeri ise bulunan değer bir dairesel döngü için olduğu için 2π’ ifadesiyle bölünmesiyle elde edilir.
Anlık Fd vektör kolu = Fπ / 2π
Fd = F / 2 olarak tespit edilir.Bulunan değer mikrometrik kağıtla ve bilgisayarda yapılan çizim sonuçlarıyla uyumludur.
ÖRNEK GÜÇ HESABI İÇİN
Şekil : 5 deki düzenegimizle sistemin bir turda Fd = F Cos²α/2 ilişkisiyle taradığı alan Şekil:6’ daki gibi olacaktır:
Bütün dairesel hareket için
Fd = F ∫ Cos²α/2 dα ifadesinden Fd = πF
Bir anlık Fd kuvvetinin de F/2 değerde olduğunu daha önce tespit etmiştik.Şimdi Şekil:6’ daki bölgeler için ayrı ayrı hesaplama yaparsak
1.bölge
Fd1 = 0----π/2 bölgesi için
Fd1 = F ∫ Cos²α/2 dα
Fd1 / F= π/4 + 1/2
2.bölge
Fd2 = π/2----π bölgesi için
Fd2 = F ∫ Cos²α/2 dα
Fd2 / F = π/4 – 1/2
3.bölge
Fd3 = π----3π/2 bölgesi için
Fd3 = F ∫ Cos²α/2 dα
Fd3 / F = π/4 – 1/2
4.bölge
Fd4 = 3π/2----2π bölgesi için
Fd4 = F ∫ Cos²α/2 dα
Fd4 / F = π/4 + 1/2
π/4 + 1/2 = 1.285398
π/4 – 1/2 = 0.2854
Bir tur için Fdt = Fd1 + Fd2 + Fd3 + Fd4 eşitliğinde ifadeleri yerine koyarsak Fdt = 3.1415 F eşitliği bulunur
Anlık Fd kuvveti için yine eşitliğin her iki tarafını 2π ile bölersek
Fd = Fdt / 2 π
Fd = 3.1415 F / 2 π
Fd = F / 2
Yine aynı sonucu buluruz.Şimdi döngüsel hareket boyunca sistemin devir sayısına da bağlı olarak kanatların anlık hızlarını bulmaya çalışalım,
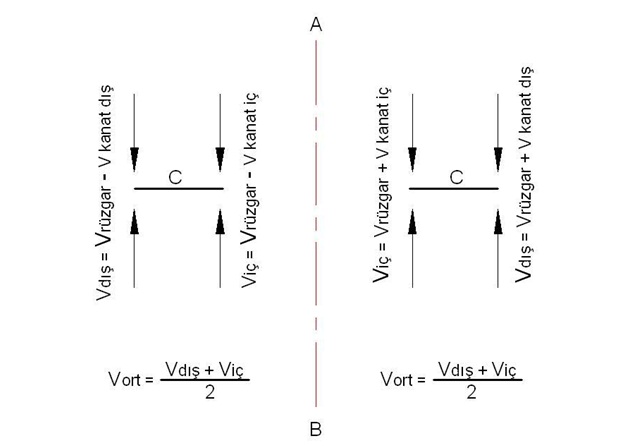
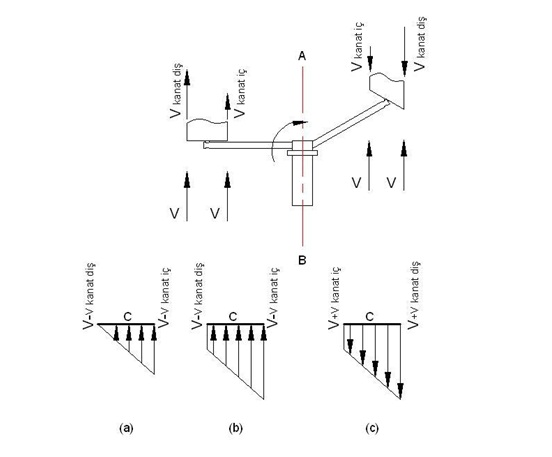
Şekil:7 yi ele alırsak kanatlar AB ekseninin sol tarafında rüzgar ile aynı yönde AB ekseninin sağ tarafında ise rüzgara karşı dönmektedir.Yine dairesel hareket boyunca kanadın dış kenarının çizgisel hızı ile iç kenarının çizgisel hızı farklı olacaktır.Kanadın dış kenarındaki hız döngüsel hareket nedeniyle daha fazla, iç kenarda ise daha azdır.Kanat yüzeyinin merkezden olan uzaklığına bağlı olarak değişen kanat yüzey konumlarındaki hızlar AB ekseninin sol kısmı için rüzgarla aynı yöndedir ve rüzgarın hızına göre izafi hız değerleri de yine kanat yüzeyi boyunca değişkenlik gösterecektir.Dolayısıyla rüzgar hızına ve kanat üzerindeki bir noktanın merkezden olan uzaklığına göre,ayrıca devir sayısına da bağlı olarak yüzeyde oluşacak güç farklı olacaktır;
Şimdi Şekil:7’ deki kanatların döngüsel hareketi ile rüzgar hızına bağlı olan izafi hızları Şekil:8’ de devir sayısına da bağlı olarak incelersek C kanat yüzeyinde oluşacak izafi hızlar Şekil : 8 (a-b-c) seçeneklerinden birine uyacaktır,burada V ile ifade edilen rüzgarın hızıdır,
Şekil:8-a/8-b/8-c durumları için
Alan
A = 1/2 ( Vk.dış + Vk.iç ) C ifadesi olur.Buradan da anlık olarak kanat yüzeyine etki eden rüzgarın hızı olarak Vort ifadesini kullanırsak
Vort = 1/2 ( Vk.dış + Vk.iç ) olur.Bütün bu irdelemeler sonucu olarak da
P = 1/2ρV²S ( V1 – V2 ) ise
P = 1/2ρV²S Vort
SAYISAL ÖRNEK
| V = 4 m/s | Rüzgar hızı |
| N = 4 | Kanat sayısı |
| C = 0.3 m | Kanat genişliği |
| H = 20 m | Kanat yüksekliği |
| 2R = 1 m | Sistemin tam çapı |
| 2L = 0.7 m | Kanat eksenleri arası mesafe |
| 2L + C/2 = 085 m | Sistemin rüzgarı karşıladığı cephe genişliği |
| Rpm = 50 min-1 | Sistemin dk.’daki devir sayısı |
Şekil:6’ da AB ekseninin sol tarafı için izafi Vort yı hesaplarsak
C kanadının dış kenarı bir devirde 4xR = 2 m yol kateder.
Vk.dış = (2 m/d) x (50 d/d) = (2 x 50) / 60 = 100/60 = 1.666 m/s
Vk.dış = 1.666 m/s
C kanadının iç kenarı bir devirde
4 x ( R –C ) = 4 x ( 0.5 – 0.3 ) = 0.8 m
Vk.iç = ( 0.8 m/d ) x ( 50 d/d ) = 40 / 60 = 0.666 m/s
Vk.iç = 0.666 m/s
Not : Bulunan bu değerler gerçeğe oldukça yakın yaklaşık değerlerdir.
AB ekseninin sol tarafı için
Vort X 2 = ( 4 - 1.666) + ( 4 – 0.666 )
Vort = 2.834 m/s
AB ekseninin sağ tarafı için
Vort X 2 = ( 4 + 0.666) + ( 4 + 1.666 )
Vort = 5.1666 m/s
AB ekseninin sol tarafı için güç
P = ( Fd1 + Fd4 ) Vort / 2π
P = ( 1,285398 F + 1,285398 F ) Vort / 2π
P = 2F ( 1.285398 ) Vort / 2π
P = 1.285398 F Vort / π
P = 0.409155 F Vort
F = 1/2ρV²S
S = N x C x H
S = 4 x ( 0.3 ) x 20 = 24 m²
F = (1.25) x ( 4 )² x ( 24 ) /2 = 240 N
P = ( 0.409155 ) ( F ) ( Vort ) = ( 0.409155 ) ( 240 ) ( 2.834 )
Psol = 278.29 Nm/s
AB ekseninin sağ tarafı için güç
P = ( Fd2 + Fd3 ) Vort / 2π
P = 2F ( 0.2854 ) Vort / 2π = 0.09085 F Vort
P = ( 0.09085 ) ( 240 ) ( 5.166 ) = 112.64 Nm/s
Psağ = 112.64 Nm/s
Sistemin toplam gücü
Ptop = Psol + Psağ
Ptop = 278.29 +112.64
Ptop = 390.93 Nm/s
Şekil : 5’ den yola çıkarak potansiyel gücü hesaplarsak
Ppotansiyel = ½ (ρVᶟS )
Spot = H ( 2L + C/2 )
Spot = 20 ( 0.85 ) = 17 m²
Ppotansiyel = ( 1.25 )( 4 )ᶟ ( 17 ) /2 = 680 Nm/s
Ppotansiyel = 680 Nm/s
Bizim sistemimizin verimi = ( 390.93 ) / ( 680 ) = 0.5749
Sistem verimi ɳ = 0.5749
Değişik rüzgar hızları ve tobloda belirtilen dikey eksenli rüzgar türbini güç ve verim hesapları yukarıdaki yöntemle hesaplanarak tablo haline getirilmiştir.
Sistem devri 50 rpm içinV (m/s) |
2R (m) |
H (m) |
C (m) |
N |
Ptop (Nm/s) |
Ppot (Nm/s) |
Verim ( ɳ ) |
4 |
1 |
20 |
0.3 |
4 |
390.93 |
680.00 |
0.5749 |
7 |
1 |
20 |
0.3 |
4 |
2299.73 |
3644.37 |
0.6310 |
8 |
1 |
20 |
0.3 |
4 |
3483.00 |
5440.00 |
0.6400 |
10 |
1 |
20 |
0.3 |
4 |
6943.36 |
10625.00 |
0.6535 |
12 |
1 |
20 |
0.3 |
4 |
12158.44 |
18360.00 |
0.6622 |
14 |
1 |
20 |
0.3 |
4 |
19489.00 |
29155.00 |
0.6685 |
16 |
1 |
20 |
0.3 |
4 |
29295.12 |
43520.00 |
0.6731 |
18 |
1 |
20 |
0.3 |
4 |
41936.60 |
61965.00 |
0.6767 |
20 |
1 |
20 |
0.3 |
4 |
57773.75 |
85000.00 |
0.6797 |
Şekil 01
Şekil 02
Şekil 03
Şekil 04
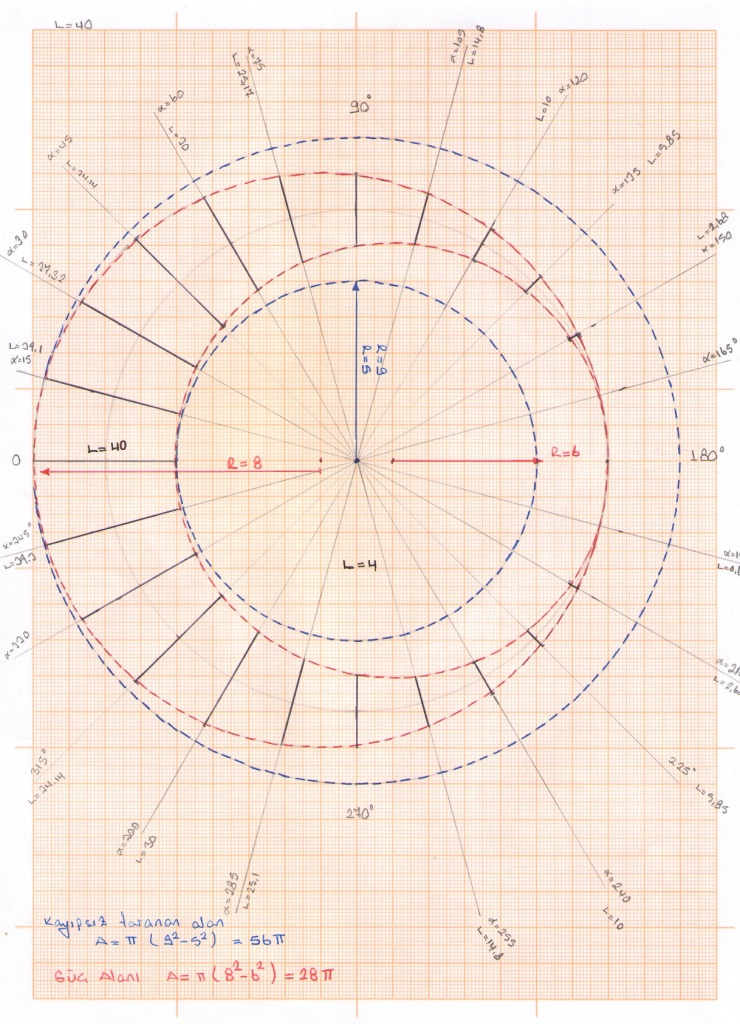
Şekil 05
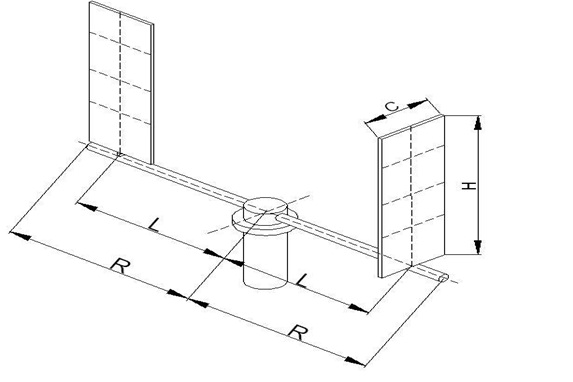
Şekil 06
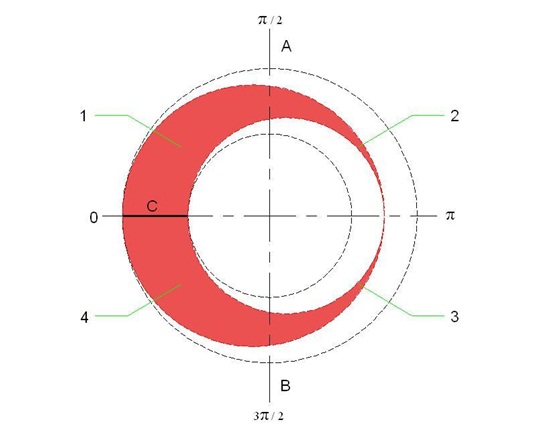
Şekil 07
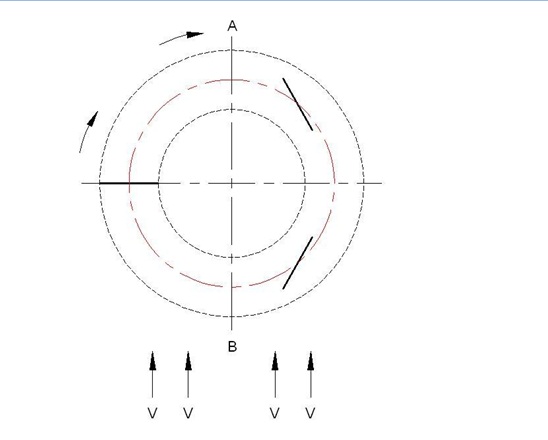
Şekil 08
Şekil 09